Applications of λ-truncations to the study of local and global solvability of nonlinear equations

Abstract

In this paper, we consider the equation in a neighbourhood of a given point 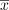, where F is a given continuous mapping between finite-dimensional real spaces. We study a class of polynomial mappings and show that these polynomials satisfy certain regularity assumptions. We show that if a λ-truncation of F at 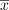¯ belongs to the considered class of polynomial mappings then for every 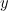close to 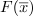there exists a solution to the equation 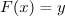that is close to 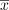. For polynomial mappings satisfying the regularity conditions we study their stability to bounded continuous perturbations.